Hoy les quiero presentar el que fue mi proyecto final de la materia de métodos numéricos en la universidad. Disfruté mucho haciéndolo. Creo que es un bonito ejemplo del proceso que hay que seguir a la hora de pasar de la teoría en papel al código.
Sería muy largo explicar el por qué de cada cachito de conocimiento utilizado en este proyecto. Lo que quiero con este post es que por lo menos se den una idea de cuáles serían los pasos a seguir si quisieran hacer algo similar. Para programar sistemas más sencillos, como una bola de billar moviéndose en línea recta o una pelota de béisbol luego de batearla, el proceso es también mucho más sencillo y no requiere tantas matemáticas. Pueden ver un ejemplo con Python aquí. Para el péndulo doble tal vez también hay métodos más sencillos, pero este es el que me sé jaja.
¡Comencemos!
Paso 1. Definir el sistema
¿Qué es un péndulo doble?
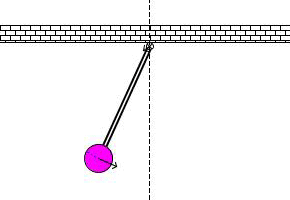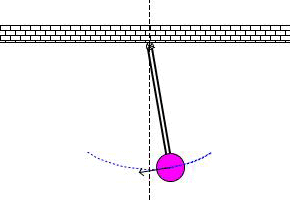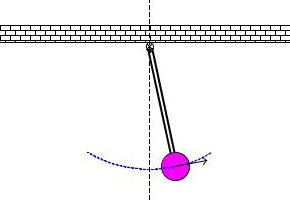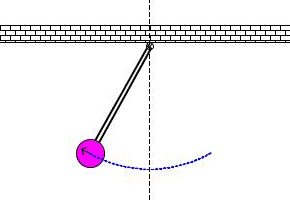
Un peńdulo simple es cualquier objeto colgando de una cuerda, moviéndose en un
sólo plano (es decir, de izquierda a derecha y de abajo hacia arriba, pero no de
atrás hacia adelante) por efecto de la gravedad. Aquí hay un gif que lo muestra:
Un péndulo doble son dos péndulos simples pegados uno al final del otro, como en
el siguiente gif:
En el gif anterior, podemos ver que el primer péndulo simple, el de arriba, traza simples arcos de circunferencia al moverse. El segundo péndulo, el de abajo, traza lo que en México conocemos como un desmadre. Por eso (spoiler alert) sus ecuaciones de movimiento son tan complicadas.
Poner nombres y hacer suposiciones
Una cosa es un péndulo real y otra es el modelo de un péndulo. En un modelo, hacemos suposiciones para que todo sea más fácil de estudiar. En la vida real, las cuerdas pesan, se curvan, se expanden y se desgastan, y la fricción con el aire frena los péndulos. En nuestro modelo, no vamos a tomar en cuenta nada de eso.
La siguiente imagen muestra todos los nombres que vamos a utilizar en el siguiente paso:
Paso 2. Encontrar las ecuaciones de movimiento
¿En dónde va a estar la bolita en cada instante de tiempo?
Una ecuación de movimiento es una fórmula matemática que te dice dónde va a estar una partícula en cada instante de tiempo. El ejemplo más simple es el de una partícula que se mueve en línea recta a velocidad constante v. Si en el segundo t = 0 la partícula se encuentra en la posición x = 0, la fórmula es x = vt. O sea que si quieres saber dónde va a estar la partícula cuando transcurran 10 segundos, sólo hay que multiplicar 10 por la velocidad y listo.
En el caso de un péndulo, es más fácil usar una sola ecuación que nos diga el ángulo que la cuerda forma con la vertical en cada instante de tiempo en lugar de dos ecuaciones que nos den las coordenadas en x y en y. En el caso del péndulo doble todo se duplica: tenemos dos ángulos y necesitamos dos ecuaciones. Son las siguientes:
g es la aceleración de la gravedad. Un puntito arriba de un ángulo significa primera derivada. Dos puntitos, segunda derivada. Las ecuaciones que incluyen derivadas se llaman ecuaciones diferenciales. Con esto ya puedes ignorar la siguiente sección y avanzar directamente al paso 3 que explica cómo resolverlas por computadora.
¿De dónde salieron esas fórmulas?
De mi corazón 🫀. Bueno,
Vienen de aplicar algo llamado “formulación de Lagrange de la mecánica clásica”. Toda la física detrás de esta formulación puede encontrarse en el libro de mecánica clásica de Thornton y Marion.
